Metode Ziegler-Nichols

Pengenalan Metode Ziegler-Nichols pada Perancangan Kontroler pada PID

Penalaan parameter kontroler PID (Proporsional Integral Diferensial) selalu didasari atas tinjauan terhadap karakteristik yang diatur (Plant). Dengan demikian betapapun rumitnya suatu plant, perilaku plant tersebut harus diketahui terlebih dahulu sebelum penalaan parameter PID itu dilakukan. Karena penyusunan model matematik plant tidak mudah, maka dikembangkan suatu metode eksperimental. Metode ini didasarkan pada reaksi plant yang dikenai suatu perubahan. Dengan menggunakan metode itu model matematik perilaku plant tidak diperlukan lagi, karena dengan menggunakan data yang berupa kurva keluaran, penalaan kontroler PID telah dapat dilakukan. Artikel berikut ini menerangkan salah satu metode pendekatan eksperimental penalaan kontroller PID, yakni metode Ziegler-Nichols serta dilengkapi dengan metode Quarter decay

Pendahuluan

Keberadaan kontroller dalam sebuah sistem kontrol mempunyai kontribusi yang besar terhadap prilaku sistem. Pada prinsipnya hal itu disebabkan oleh tidak dapat diubahnya komponen penyusun sistem tersebut. Artinya, karakteristik plant harus diterima sebagaimana adanya, sehingga perubahan perilaku sistem hanya dapat dilakukan melalui penambahan suatu sub sistem, yaitu kontroler.

Salah satu tugas komponen kontroler adalah mereduksi sinyal kesalahan, yaitu perbedaan antara sinyal setting dan sinyal aktual. Hal ini sesuai dengan tujuan sistem kontrol adalah mendapatkan sinyal aktual senantiasa (diinginkan) sama dengan sinyal setting. Semakin cepat reaksi sistem mengikuti sinyal aktual dan semakin kecil kesalahan yang terjadi, semakin baiklah kinerja sistem kontrol yang diterapkan.

Apabila perbedaan antara nilai setting dengan nilai keluaran relatif besar, maka kontroler yang baik seharusnya mampu mengamati perbedaan ini untuk segera menghasilkan sinyal keluaran untuk mempengaruhi plant. Dengan demikian sistem secara cepat mengubah keluaran plant sampai diperoleh selisih antara setting dengan besaran yang diatur sekecil mungkin[Rusli, 1997].

Kontroler Proposional

Kontroler proposional memiliki keluaran yang sebanding/proposional dengan besarnya sinyal kesalahan (selisih antara besaran yang diinginkan dengan harga aktualnya) [Sharon, 1992, 19]. Secara lebih sederhana dapat dikatakan, bahwa keluaran kontroller proporsional merupakan perkalian antara konstanta proporsional dengan masukannya. Perubahan pada sinyal masukan akan segera menyebabkan sistem secara langsung mengubah keluarannya sebesar konstanta pengalinya.

Gambar 1 menunjukkan blok diagram yang menggambarkan hubungan antara besaran setting, besaran aktual dengan besaran keluaran kontroller proporsional. Sinyal keasalahan (error) merupakan selisih antara besaran setting dengan besaran aktualmya. Selisih ini akan mempengaruhi kontroller, untuk mengeluarkan sinyal positip (mempercepat pencapaian harga setting) atau negatif (memperlambat tercapainya harga yang diinginkan).

Gambar 1 Diagram blok kontroler proporsional

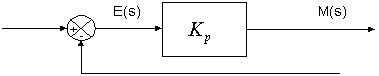
Kontroler proporsional memiliki 2 parameter, pita proporsional (proportional band) dan konstanta proporsional. Daerah kerja kontroller efektif dicerminkan oleh Pita proporsional (Gunterus, 1994, 6-24), sedangkan konstanta proporsional menunjukkan nilai faktor penguatan terhadap sinyal kesalahan, K_p.

Hubungan antara pita proporsional (PB) dengan konstanta proporsional (K_p) ditunjukkan secara prosentasi oleh persamaan berikut:

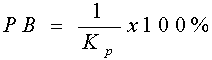
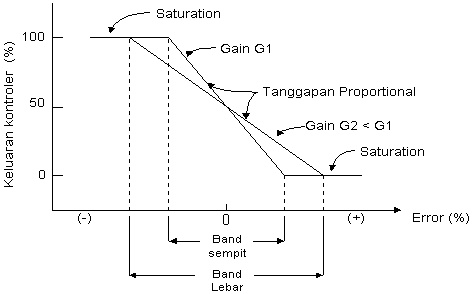
Gambar 2 menunjukkan grafik hubungan antara PB, keluaran kontroler dan kesalahan yang merupakan masukan kontroller. Ketika konstanta proporsional bertambah semakin tinggi, pita proporsional menunjukkan penurunan yang semakin kecil, sehingga lingkup kerja yang dikuatkan akan semakin sempit[Johnson, 1988, 372].

Gambar 2: Proportional band dari kontroler proporsional tergantung pada penguatan.

Ciri-ciri kontroler proporsional harus diperhatikan ketika kontroler tersebut diterapkan pada suatu sistem. Secara eksperimen, pengguna kontroller proporsional harus memperhatikan ketentuan-ketentuan berikut ini:

1. Kalau nilai K_p kecil, kontroler proporsional hanya mampu melakukan koreksi kesalahan yang kecil, sehingga akan menghasilkan respon sistem yang lambat.
2. Kalau nilai K_p dinaikkan, respon sistem menunjukkan semakin cepat mencapai keadaan mantabnya.
3. Namun jika nilai K_p diperbesar sehingga mencapai harga yang berlebihan, akan mengakibatkan sistem bekerja tidak stabil, atau respon sistem akan berosilasi [Pakpahan, 1988, 193].

Kontroler Integral

Kontroller integral berfungsi menghasilkan respon sistem yang memiliki kesalahan keadaan mantap nol. Kalau sebuah plant tidak memiliki unsur integrator (1/s ), kontroller proporsional tidak akan mampu menjamin keluaran sistem dengan kesalahan keadaan mantabnya nol. Dengan kontroller integral, respon sistem dapat diperbaiki, yaitu mempunyai kesalahan keadaan mantapnya nol.

Kontroler integral memiliki karakteristik seperti halnya sebuah integral. Keluaran kontroller sangat dipengaruhi oleh perubahan yang sebanding dengan nilai sinyal kesalahan(Rusli, 18, 1997). Keluaran kontroler ini merupakan jumlahan yang terus menerus dari perubahan masukannya. Kalau sinyal kesalahan tidak mengalami perubahan, keluaran akan menjaga keadaan seperti sebelum terjadinya perubahan masukan.

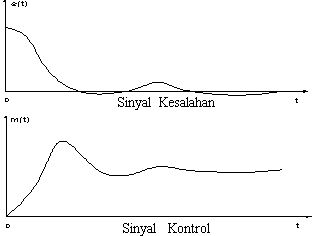
Sinyal keluaran kontroler integral merupakan luas bidang yang dibentuk oleh kurva kesalahan penggerak- lihat konsep numerik. Sinyal keluaran akan berharga sama dengan harga sebelumnya ketika sinyal kesalahan berharga nol. Gambar 3 [Ogata, 1997, 236] menunjukkan contoh sinyal kesalahan yang disulutkan ke dalam kontroller integral dan keluaran kontroller integral terhadap perubahan sinyal kesalahan tersebut.

Gambar 3 Kurva sinyal kesalahan e(t) terhadap t dan kurva u(t) terhadap t pada pembangkit kesalahan nol.

Gambar 4 menunjukkan blok diagram antara besaran kesalahan dengan keluaran suatu kontroller integral.

Gambar 4: Blok diagram hubungan antara besaran kesalahan dengan kontroller integral
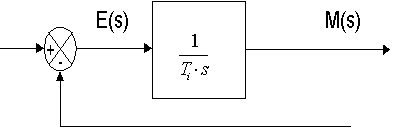
Pengaruh perubahan konstanta integral terhadap keluaran integral ditunjukkan oleh Gambar 5. Ketika sinyal kesalahan berlipat ganda, maka nilai laju perubahan keluaran kontroler berubah menjadi dua kali dari semula. Jika nilai konstanta integrator berubah menjadi lebih besar, sinyal kesalahan yang relatif kecil dapat mengakibatkan laju keluaran menjadi besar (Johnson, 1993, 375).

Gambar 5 Perubahan keluaran sebagai akibat penguatan dan kesalahan

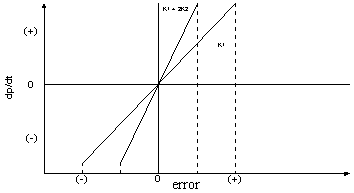
Ketika digunakan, kontroler integral mempunyai beberapa karakteristik berikut ini:

1. Keluaran kontroler membutuhkan selang waktu tertentu, sehingga kontroler integral cenderung memperlambat respon.
2. Ketika sinyal kesalahan berharga nol, keluaran kontroler akan bertahan pada nilai sebelumnya.
3. Jika sinyal kesalahan tidak berharga nol, keluaran akan menunjukkan kenaikan atau penurunan yang dipengaruhi oleh besarnya sinyal kesalahan dan nilai K_i (Johnson, 1993, 376).
4. Konstanta integral K_i yang berharga besar akan mempercepat hilangnya offset. Tetapi semakin besar nilai konstanta K_i akan mengakibatkan peningkatan osilasi dari sinyal keluaran kontroler (Guterus, 1994, 7-4).

Kontroler Diferensial

Keluaran kontroler diferensial memiliki sifat seperti halnya suatu operasi derivatif. Perubahan yang mendadak pada masukan kontroler, akan mengakibatkan perubahan yang sangat besar dan cepat. Gambar 6 menunjukkan blok diagram yang menggambarkan hubungan antara sinyal kesalahan dengan keluaran kontroller.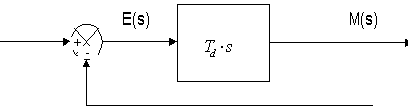 Gambar 6: BlokDiagram kontroler diferensial

Gambar 7 menyatakan hubungan antara sinyal masukan dengan sinyal keluaran kontroler diferensial. Ketika masukannya tidak mengalami perubahan, keluaran kontroler juga tidak mengalami perubahan, sedangkan apabila sinyal masukan berubah mendadak dan menaik (berbentuk fungsi step), keluaran menghasilkan sinyal berbentuk impuls. Jika sinyal masukan berubah naik secara perlahan (fungsi ramp), keluarannya justru merupakan fungsi step yang besar magnitudnya sangat dipengaruhi oleh kecepatan naik dari fungsi ramp dan faktor konstanta diferensialnya T_d (Guterus, 1994, 8-4).

Gambar 7 Kurva waktu hubungan input-output kontroler diferensial

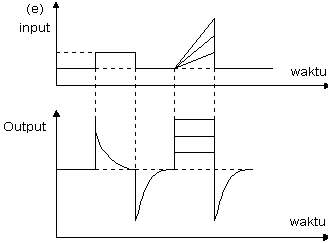
Karakteristik kontroler diferensial adalah sebagai berikut:

1. Kontroler ini tidak dapat menghasilkan keluaran bila tidak ada perubahan pada masukannya (berupa sinyal kesalahan).
2. Jika sinyal kesalahan berubah terhadap waktu, maka keluaran yang dihasilkan kontroler tergantung pada nilai Td dan laju perubahan sinyal kesalahan. (Powel, 1994, 184).
3. Kontroler diferensial mempunyai suatu karakter untuk mendahului, sehingga kontroler ini dapat menghasilkan koreksi yang signifikan sebelum pembangkit kesalahan menjadi sangat besar. Jadi kontroler diferensial dapat mengantisipasi pembangkit kesalahan, memberikan aksi yang bersifat korektif, dan cenderung meningkatkan stabilitas sistem (Ogata,, 1997, 240).

Berdasarkan karakteristik kontroler tersebut, kontroler diferensial umumnya dipakai untuk mempercepat respon awal suatu sistem, tetapi tidak memperkecil kesalahan pada keadaan tunaknya. Kerja kontrolller diferensial hanyalah efektif pada lingkup yang sempit, yaitu pada periode peralihan. Oleh sebab itu kontroler diferensial tidak pernah digunakan tanpa ada kontroler lain sebuah sistem (Sutrisno, 1990, 102).

Kontroler PID

Setiap kekurangan dan kelebihan dari masing-masing kontroler P, I dan D dapat saling menutupi dengan menggabungkan ketiganya secara paralel menjadi kontroler proposional plus integral plus diferensial (kontroller PID). Elemen-elemen kontroller P, I dan D masing-masing secara keseluruhan bertujuan untuk mempercepat reaksi sebuah sistem, menghilangkan offset dan menghasilkan perubahan awal yang besar(Guterus, 1994, 8-10).

Gambar 8 menunjukkan blok diagram kontroler PID.

Gambar 8 Blok diagram kontroler PID analog

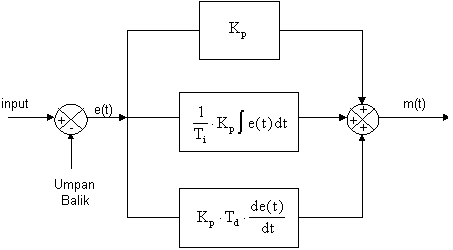
Keluaran kontroller PID merupakan jumlahan dari keluaran kontroler proporsional, keluaran kontroler integral. Gambar 9 menunjukkan hubungan tersebut.

Gambar 9 Hubungan dalam fungsi waktu antara sinyal keluaran dengan masukan untuk kontroller PID

Karakteristik kontroler PID sangat dipengaruhi oleh kontribusi besar dari ketiga parameter P, I dan D. Penyetelan konstanta Kp, Ti, dan Td akan mengakibatkan penonjolan sifat dari masing-masing elemen. Satu atau dua dari ketiga konstanta tersebut dapat disetel lebih menonjol dibanding yang lain. Konstanta yang menonjol itulah akan memberikan kontribusi pengaruh pada respon sistem secara keseluruhan (Gunterus, 1994, 8-10).

Penalaan Paramater Kontroler PID

Penalaan parameter kontroller PID selalu didasari atas tinjauan terhadap karakteristik yang diatur (Plant). Dengan demikian betapapun rumitnya suatu plant, perilaku plant tersebut harus diketahui terlebih dahulu sebelum penalaan parameter PID itu dilakukan. Karena penyusunan model matematik plant tidak mudah, maka dikembangkan suatu metode eksperimental. Metode ini didasarkan pada reaksi plant yang dikenai suatu perubahan. Dengan menggunakan metode itu model matematik perilaku plant tidak diperlukan lagi, karena dengan menggunakan data yang berupa kurva krluaran, penalaan kontroler PID telah dapat dilakukan. Penalaan bertujuan untuk mendapatkan kinerja sistem sesuai spesifikasi perancangan. Ogata menyatakan hal itu sebagai alat control (controller tuning) (Ogata, 1997, 168, Jilid 2). Dua metode pendekatan eksperimen adalah Ziegler-Nichols dan metode Quarter decay.

Metode Ziegler-Nichols

Ziegler-Nichols pertama kali memperkenalkan metodenya pada tahun 1942. Metode ini memiliki dua cara, metode osilasi dan kurva reaksi. Kedua metode ditujukan untuk menghasilkan respon sistem dengan lonjakan maksimum sebesar 25%. Gambar 11 memperlihatkan kurva dengan lonjakan 25%.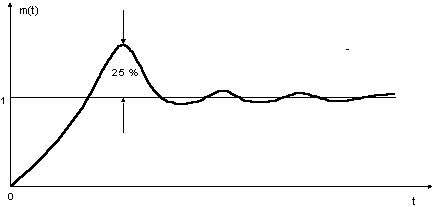
Gambar 11 Kurva respons tangga satuan yang memperlihatkan 25 % lonjakan maksimum

Metode Kurva Reaksi

Metode ini didasarkan terhadap reaksi sistem untaian terbuka. Plant sebagai untaian terbuka dikenai sinyal fungsi tangga satuan (gambar 12). Kalau plant minimal tidak mengandung unsur integrator ataupun pole-pole kompleks, reaksi sistem akan berbentuk S. Gambar 13 menunjukkan kurva berbentuk S tersebut. Kelemahan metode ini terletak pada ketidakmampuannya untuk plant integrator maupun plantt yang memiliki pole kompleks.
Gambar 12 Respon tangga satuan sistem Gambar 13 Kurva Respons berbentuk S.

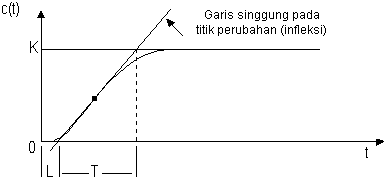
Kurva berbentuk-s mempunyai dua konstanta, waktu mati (dead time) L dan waktu tunda T. Dari gambar 13 terlihat bahwa kurva reaksi berubah naik, setelah selang waktu L. Sedangkan waktu tunda menggambarkan perubahan kurva setelah mencapai 66% dari keadaan mantapnya. Pada kurva dibuat suatu garis yang bersinggungan dengan garis kurva. Garis singgung itu akan memotong dengan sumbu absis dan garis maksimum. Perpotongan garis singgung dengan sumbu absis merupakan ukuran waktu mati, dan perpotongan dengan garis maksimum merupakan waktu tunda yang diukur dari titik waktu L.

Penalaan parameter PID didasarkan perolehan kedua konstanta itu. Zeigler dan Nichols melakukan eksperimen dan menyarankan parameter penyetelan nilai Kp, Ti, dan Td dengan didasarkan pada kedua parameter tersebut. Tabel 1 merupakan rumusan penalaan parameter PID berdasarkan cara kurva reaksi.

Tabel 1 Penalaan paramater PID dengan metode kurva reaksi

Tipe Kontroler	Kp	Ti	Td
P	T/L	~	0
PI	0,9 T/L	L/0.3	0
PID	1,2 T/L	2L	0,5L

Metode Osilasi

Metode ini didasarkan pada reaksi sistem untaian tertutup. Plant disusun serial dengan kontroller PID. Semula parameter parameter integrator disetel tak berhingga dan parameter diferensial disetel nol (T_i = ~ ;T_d = 0). Parameter proporsional kemudian dinaikkan bertahap. Mulai dari nol sampai mencapai harga yang mengakibatkan reaksi sistem berosilasi. Reaksi sistem harus berosilasi dengan magnitud tetap(Sustain oscillation) (Guterus, 1994, 9-9). Gambar 14 menunjukkan rangkaian untaian tertutup pada cara osilasi.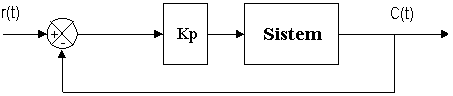 Gambar 14 Sistem untaian tertutup dengan alat kontrol proporsional

Nilai penguatan proportional pada saat sistem mencapai kondisi sustain oscillation disebut ultimate gain K_u. Periode dari sustained oscillation disebut ultimate period T_u (Perdikaris, 1991, 433). Gambar 15 menggambarkan kurva reaksi untaian terttutup ketika berosilasi.

Gambar 15 Kurva respon sustain oscillation

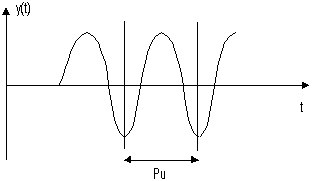
Penalaan parameter PID didasarkan terhadap kedua konstanta hasil eksperimen, Ku dan Pu. Ziegler dan Nichols menyarankan penyetelan nilai parameter K_p, T_i, dan T_d berdasarkan rumus yang diperlihatkan pada Tabel 2.

Tabel 2 Penalaan paramater PID dengan metode osilasi

Tipe Kontroler	Kp	Ti	Td
P	0,5.Ku
PI	0,45.Ku	1/2 Pu
PID	0,6.Ku	0,5 Pu	0,125 Pu

Metode Quarter - decay

Karena tidak semua proses dapat mentolerir keadaan osilasi dengan amplituda tetap, Cohen-coon berupaya memperbaiki metode osilasi dengan menggunakan metode quarter amplitude decay. Tanggapan untaian tertutup sistem, pada metode ini, dibuat sehingga respon berbentuk quarter amplitude decay (Guterus, 1994, 9-13). Quarter amplitude decay didefinisikan sebagai respon transien yang amplitudanya dalam periode pertama memiliki perbandingan sebesar seperempat (1/4) (Perdikaris, 1991, 434).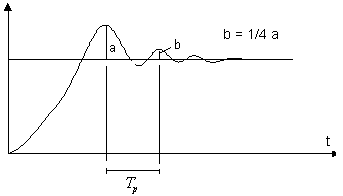 Gambar 16 Kurva respon quarter amplitude decay

Kontroler proportional K_p ditala hingga diperoleh tanggapan quarter amplitude decay, periode pada saat tanggapan ini disebut T_p dan parameter T_i dan T_d dihitung dari hubungan (Perdikaris, 434, 1990). Sedangkan penalaan parameter kontroler PID adalah sama dengan yang digunakan pada metode Ziegler-Nichols (lihat tabel 1 - untuk metode kurva reaksi dan tabel 2 untuk metode osilasi).

Bersambung pada artikel

Kontroler PID-Ziegler-Nichols pada Sistem Kontrol posisi berbasis komputer IBM-PC.

Daftar Pustaka

1. Rusli, Mohammad: 1997, Sistem Kontrol kedua, Malang: Teknik Elektro -Universitas Brawijaya
2. Rameli, Mochammad, Rusdhianto E., Djoko Susilo: Sistem Pengaturan Malang, 1996
3. Ziegler, J. G. dan N.B. Nichols, 1942, Optimum Setting for Automatic Controllers, Tans. ASME, vol. 64, pp. 759-768
4. Gunterus, Frans: Falsafah Dasar: Sistem Pengendalian Proses, jakarta: PT. Elex Media Komputindo, Jakarta, 1994
5. Johnson, Curtis: Process Control Instrumentation Technology, Englewood Cliffs, New Jersey, 1988
6. Ogata, Katsuhiko: Teknik Kontrol Automatik – terjemahan: Ir. Edi Laksono, Erlangga, Jakarta, 1991